Inverse Trigonometric Functions Class 12 Important Questions with Solutions Previous Year Questions
Question 1.
Write the value of
tan-1 (√3) – cot-1 (- √3). (All India 2019,13)
Answer:
We have, tan-1 (√3) – cot-1 (-√3)
= tan-1 (√3) – {π – cot-1 (√3)} [∵ cot-1 (- x) = π – cot-1 x; x ∈ R]
= tan-1 √3 – π + cot-1 √3
= (tan-1 √3 + cot-1 √3) – π
= π2 – π = – π2 [∵ tan-1x + cot-1x = π2; x ∈ R]
Which is the required principal value.
Question 2.
Find the principal value of
tan-1√3 – sec-1 (- 2). (CBSE 2018 C; All India 2012)
Answer:
We have, tan-1√3 – sec-1 (- 2)
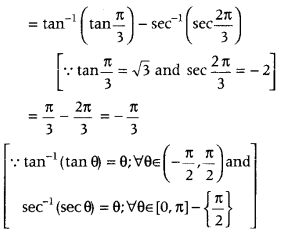
Which is the required principal value.
Question 3.
If sin (sin-115 + cos-1x) = 1, then find the value of x. (Delhi 2014)
Answer:
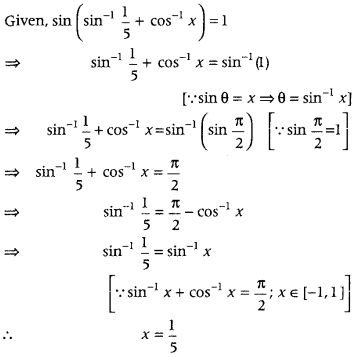
Question 4.
If tan-1x + tan-1 y = π4; xy < 1, then write the value of x + y + xy. (All India 2014)
Answer:
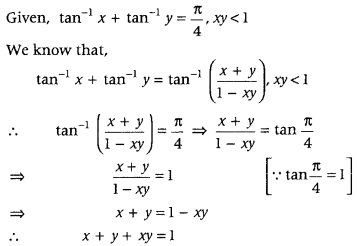
Question 5.
Write the value of cos-1(−12) + 2 sin-1(12). (Foreign 2014)
Answer:
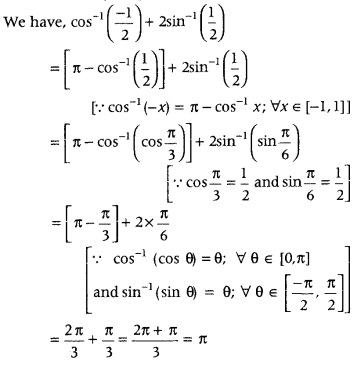
Question 6.
Write the principal value of cos-1 [cos(680)°]. (Delhi 2014C)
Answer:
First we check the given angle lies in the principal value branch. If it is so, then use the property cos1 (cos θ) = θ, ∀θ ∈ [0, 180°]. Otherwise reduce the angle such that, it lies in principal value branch.
We know that, principal value branch of cos-1 x is [0, 180°].
Since, 680° ∉ [0, 180°], so write 680° as 2 × 360° – 40°
Now, cos-1 [cos(680)°] = cos-1 [cos(2 × 360° – 40°)]
= cos-1 (cos 4o°) [∵ cos(4π – θ) = cos θ]
Since, 40° ∈ [0, 180°]
∴ cos-1[cos(680°)] = 40° [∵ cos-1 (cos θ) = θ; ∀ θ ∈ [0, 1 80°]]
which is the required principal value.
Question 7.
Write the principal value of tan-1[sin(−π2)]. (All India 2014C)
Answer:
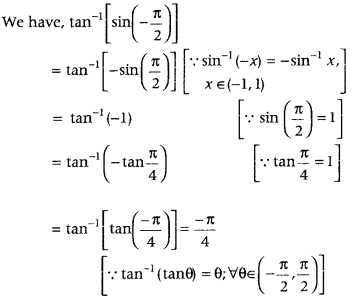
which is the required principal value.
Question 8.
Find the value of the following.
cot (π2 – 2 cot-1√3) (All India 2014C)
Answer:
First, use cot(π2−θ) = tan θ, then put
cot-1 √3 = π6 and simplify it .
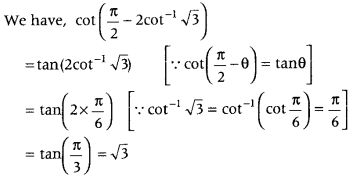
Question 9.
Write the principal value of the following.
[cos−13√2+cos−1(−12)] (Delhi 2013C)
Answer:
Question 10.
Write the principal value of
tan-1 (1) + cos-1(−12). (Delhi 2013)
Answer:
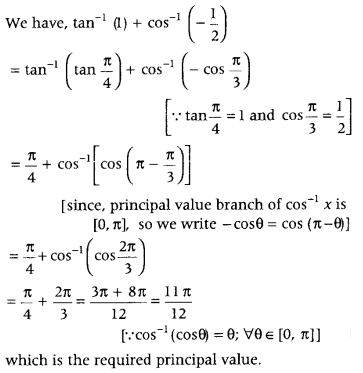
Alternate Method:
We have
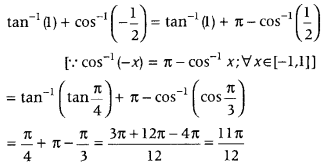
which is the required principal value.
Question 11.
Write the value of tan (2 tan-115). (Delhi 2013)
Answer:
We have,
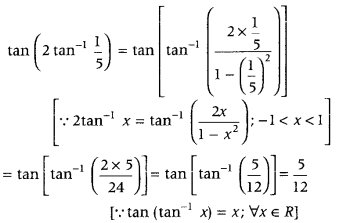
Question 12.
Write the value of
tan-1[2sin(2cos−13√2)]. (All India 2013)
Answer:
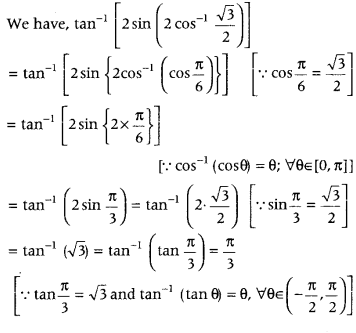
Question 13.
Write the value of cos-1 (12) – 2 sin-1 (12). (DeIh 2012)
Answer:
2π3
Question 14.
Using the principal values, write the value of cos-1(12) + 2 sin-1(12).
Answer:
2π3
Question 15.
Write the value of sin [π3−sin−1(−12)] (Delhi 2011).
Answer:
We have,
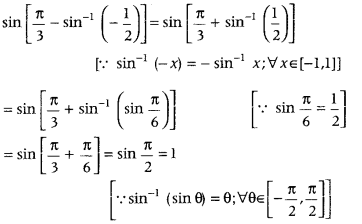
Question 16.
Write the value of tan-1(tan 3π4). (Delhi 2011)
Answer:
First, we check the given angle lies in the principal value branch. If it is so, then use the property tan-1 (tan θ) = θ, ∀ θ ∈ (−π2,π2), Otherwise reduce the angle such that it lies in principal value branch.
We know that, principal value branch of tan-1 x is (−π2,π2).
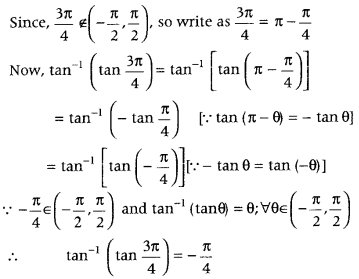
Question 17.
Write the value of cos-1 (cos 7π6). (Delhi 2011, 2009; All India 2009)
Answer:
We know that, the principal value branch of cos-1x is [0, π].
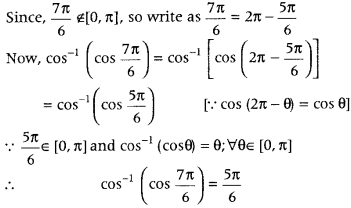
Question 18.
What is the principal value of
cos-1(cos2π3) + sin-1(sin2π3)? (All India 2011, 2009C. 2008)
Answer:
We know that, the principal value branch of cos-1 x is [0, π] and for sin-1 x is [−π2,π2].
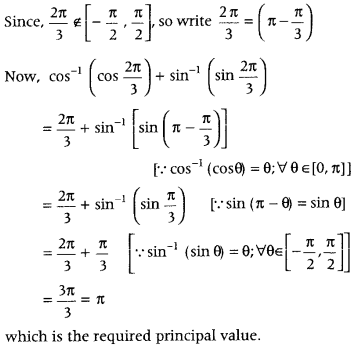
Question 19.
What is the principal value of tan-1 (- 1)? (Foreign 2011, 2o08c)
Answer:
We have,
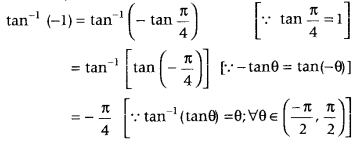
Which is the required principal value.
Alternate Method:
We have,
tan-1 (-1) = – tan-1 (1) [∵ tan-1 x; x ∈ R]
= – tan-1(tan π4) [∵ tan π4 = 1]
= −π4 [∵ tan-1 (tan θ) = θ; ∀ θ ∈ (−π2,π2)]
which is the required principal value.
Question 20.
Using the principal values, write the value of sin-1(−3√2). (All India 2011C, Delhi 2010)
Answer:
We have

Question 21.
Write the principal value of sin-1(−12). (Delhi 2010)
Answer:
– π6
Question 22.
What is the principal value of sin-1 (- 2)? (All India 2010)
Answer:
We have, sec-1 (-2) = π – sec-1 (2)
[∵ sec-1 (- x) = π – sec-1 (x); |x| ≥ 1
= π – sec-1(sec π3) = π – π3
[∵ sec π3 = 2 and sec-1 (sec θ) = θ; ∀ θ ∈ [0, π] – {π2}]
= 2π3
which is the required principal value.
Question 23.
What is the domain of the function sin-1 x? (Foregin 2010)
Answer:
The domain of the function sin-1 x is [-1, 1].
Question 24.
Using the principal values, find the value of cos-1(cos13π6). (All India 2010C ).
Answer:
π6
Question 25.
If tan-1 (√3) + cot-1 x = π2‚ then find the value of x. (All India 2010C)
Answer:
Given, tan-1 √3 + cot-1 x = π2
⇒ tan-1 √3 = π2 – cot-1 x
⇒ tan-1 √3 = tan-1 x
[∵ tan-1 x + cot-1 x = π2; x ∈ R]
∴ x = √3
Question 26.
Prove that
3 sin-1x = sin-1(3x – 4x3), x ∈ [−12,12]. (CBSE 2018)
Answer:
Consider, RHS = sin-1 (3x – 4x3) ……(i)
Let x = sin θ,
then θ = sin-1 x
Now, from Eq. (i), we get
RHS = sin-1 (3 sin θ – 4 sin3 θ)
= sin-1 (sin 3 θ) [∵ sin 3A = 3sin A – 4sin3 A]
= 3θ
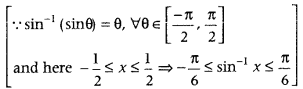
= 3 sin-1 x [∵ θ = sin-1 x]
= LHS
Hence Proved.
Question 27.
Prove that
3 cos-1x = cos-1(4x3 – 3x), x ∈[12,1].
Answer:
Consider, RHS = cos-1 (4x3 – 3x)
Let x = cos θ ⇒ θ = cos-1 x
Now, from Eq. (1), we get
RHS = cos-1 (4 cos3 θ – 3 cos θ)
= cos-1 (cos 3θ) [∵ cos 3A = 4 cos3 A – 3 cos A]
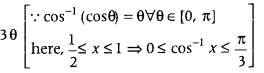
= 3 cos-1 x
= LHS
Hence proved.
Question 28.
Solve for X,
tan-1 (x + 1) + tan-1 (x – 1) = tan-1831. (All India 2019,15)
Answer:
First, use the formula tan-1 x + tan-1 y = tan-1(x+y1−xy); xy < 1, then simplify it and get the values of x. Further, verify the given equation by obtained values of x.
Given, tan-1(x + 1) + tan-1(x – 1) = tan-1 831 …… (i)
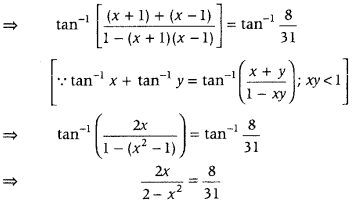
⇒ 62x = 16 – 8x2
⇒ 8x2 + 62x – 16 = 0
⇒ 4x2 + 31x – 8 = 0
⇒ 4x2 + 32x – x – 8 = 0
⇒ 4x(x + 8) – 1 (x + 8) = 0
⇒ (x + 8) (4x – 1) = 0
∴ x = -8 or x = 14
But x = – 8 gives LHS = tan-1 (- 7) + tan-1 (- 9)
= – tan-1 (7) – tan-1 (9),
which is negative, while RHS is positive.
So, x = – 8 is not possible.
Hence, x = 14 is the only solution of the given equation.
Question 29.
Find the value of sin (cos-1 + tan-123). (All India 2019)
Answer:
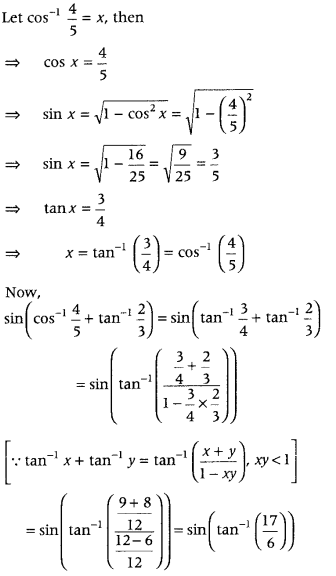
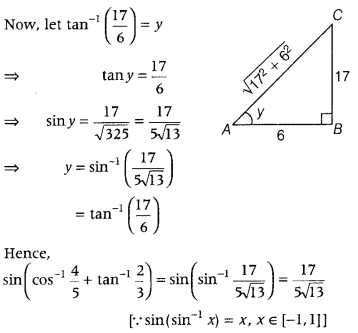
Question 30.
Solve for x, tan-1 3x + tan-1 2x = π4. (Delhi 2019. 2015, 2013C)
Answer:
Given, tan-1 3x + tan-1 2x = π4 …………. (i)
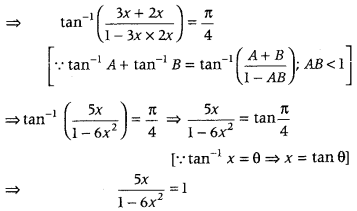
⇒ 5x = 1 – 6x2
⇒ 6x2 + 5x – 1 = 0
⇒ 6x2 + 6x – x – 1 = 0
⇒ 6x(x + 1) – 1(x + 1) = 0
⇒ (6x – 1) (x + 1) = 0
⇒ 6x – 1 = 0 or x + 1 = 0
∴ x = 16 or x = – 1
But x = – 1 does not satisfy the Eq. (1). as LHS becomes negative. So, x = 16 is the only solution of the given equation.
Question 31.
Solve tan-1 4x + tan-1 6x = π4 (Delhi 2019)
Answer:
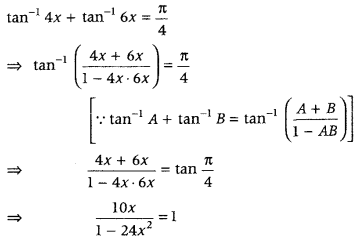
⇒ 10x = 1 – 24x2
⇒ 24x2 + 10x – 1 = 0
⇒ 24x2 + 12x – 2x – 1 = 0
⇒ 12x(2x + 1) – 1 (2x + 1) = 0
⇒ (2x + 1) (12x – 1) = 0
⇒ 2x + 1 = 0
x = – 12
or 12x – 1 = 0
x = 112
But x = – 12 does not satisfy the given equation.
Hence, the required solution is x = 112
Question 32.
If tan-1x−3x−4 + tan x+3x+4=π4, then find the value of x. (All India 2017)
Answer:
Given
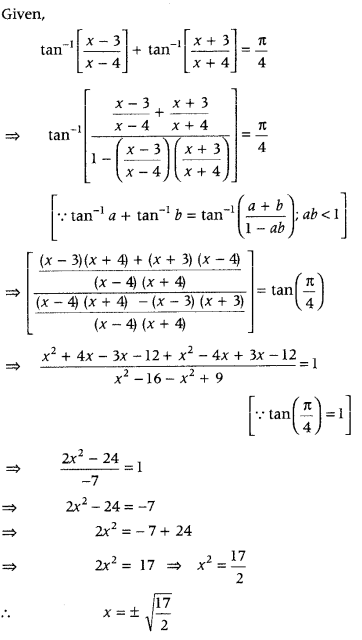
Question 33.
Prove that tan{π4+12cos−1ab} + tan{π4−12cos−1(ab)} = 2ba.
Answer:
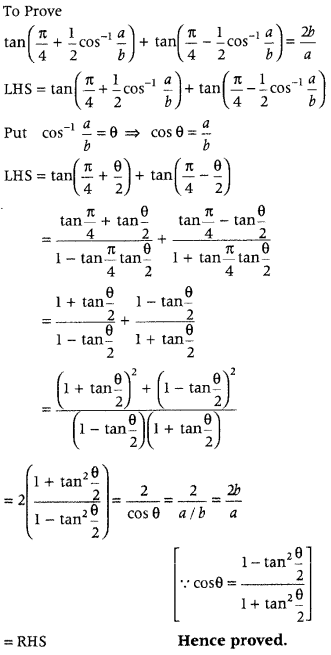
Question 34.
Solve the following equation for x.
cos(tan-1 x) = sin(cot-134) (Delhi 2017, Foregin 2014; All India 2013)
Answer:
We have, cos(tan-1 x) = sin(cot– 1 34) …….. (i)
Let tan-1 x = θ and cot-134 = Φ ∀θ ∈ (−π2,π2)
and Φ ∈ (0, π)
⇒ tan θ = x and cot Φ = 34
⇒ sec θ = 1+tan2θ−−−−−−−−√ and cosec Φ = 1+cot2ϕ−−−−−−−−√
[taking positive square root as θ ∈ (−π2,π2) and Φ ∈ (θ, π)]
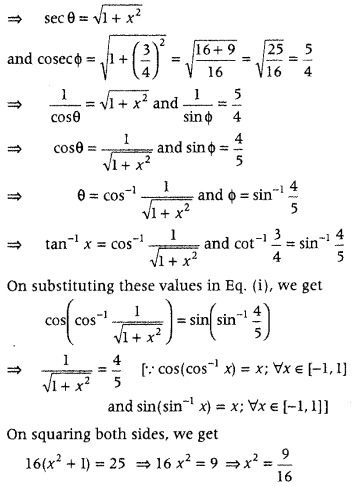
⇒ x = ± 34 [taking square root both sides]
But x = −34 does not satisfy the given equation. Hence, the required solution is x = 34.
Question 35.
Prove that
tan−115+tan−117+tan−113+tan−118=π4 (DelhI 2018; Foreign 2015; Delhi 2008; 2008C)
Answer:
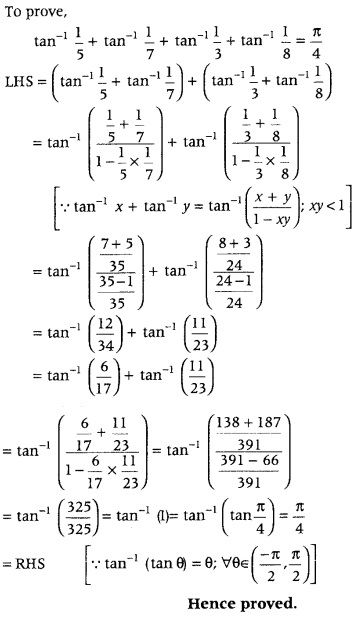
Question 36.
Solve for x,
2 tan-1x (cos x) = tan-1 (2 cosecx). (Delhi 2016; Foreign 2015, Delhi 2014C; All India 2009)
Answer:
Given equation is
2 tan-1 (cos x) = tan-1 (2 cosec x)
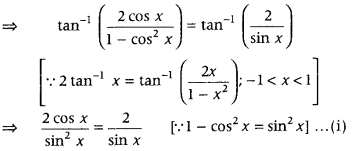
⇒ sin x cos x – sin2 x = 0
⇒ sin x (cos x – sin x) = 0
⇒ sin x = 0 or cos x = sin x
⇒ sin x = sin 0
or cot x = 1 = cot π4
∴ x = 0 or π4
But here at x = 0, the given equation does not exist.
Hence, x = π4 is the only solution.
Question 37.
Solve for x,
tan-1(x – 1) + tan-1 x + tan-1(x + 1) = tan-1 3x (All India 2016)
Answer:
Given,
tan-1 (x – 1) + tan-1 x + tan-1 (x + 1) = tan-1 3x
⇒ tan-1 (x – 1) + tan-1 (x + 1) = tan-1 3x – tan-1 x
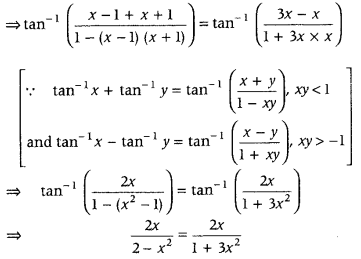
⇒ 2x(1 + 3x2) = 2x(2 – x2)
⇒ 2x[1 + 3x2 – (2 – x2)] = 0
⇒ x(4x2 – 1) = 0 ⇒ x = 0 or 4x2 – 1 = 0
∴ x = 0 or x = ± 12
Question 38.
Prove that
tan-1(6x−8x31−12x2) – tan-1(4x1−4x2) = tan-1 2x; |2x| < 13√. (All India 2016)
Answer:

Question 39.
Prove that
cot-1(1+sinx√+1−sinx√1+sinx√−1−sinx√) = x2, 0 < x < π2, or x ∈ π4
(Foreign 2016; Delhi 2014, 2011; All India 2009)
Answer:
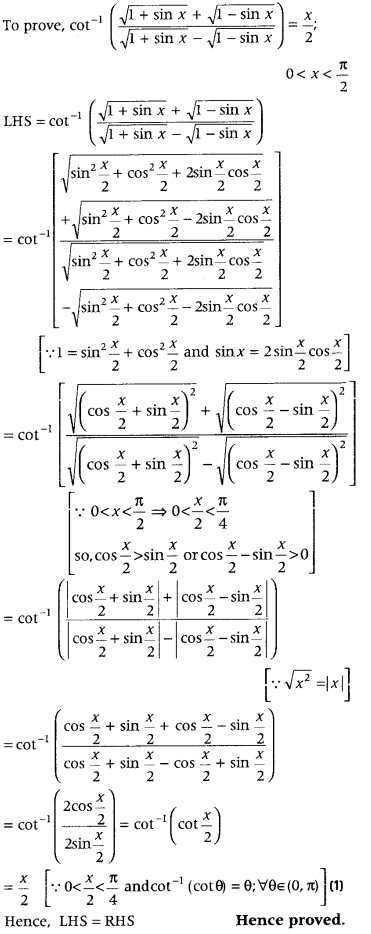
Alternate Method:
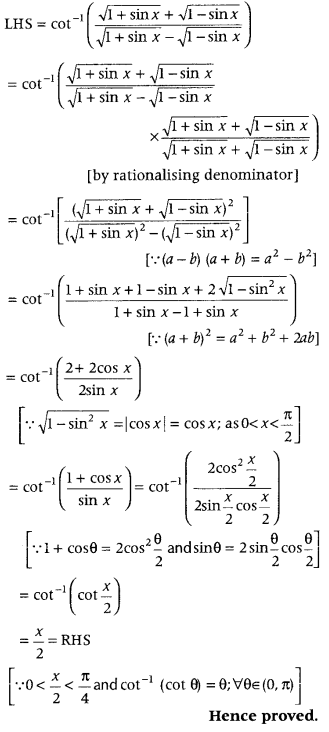
Question 40.
Solve for x,
tan-1(x−2x−1) – tan-1(x+2x+1) = π4 (Foreign 2016)
Answer:
72−−√,−72−−√
Question 41.
If sin [cot-1 (x + 1)] = cos (tan-1 x), then find x. (Delhi 2015)
Answer:
– 12
Question 42.
If(tan-1 x)2 + (cot-1 x)2 = 5π28, then find x. (Delhi 2015)
Answer:
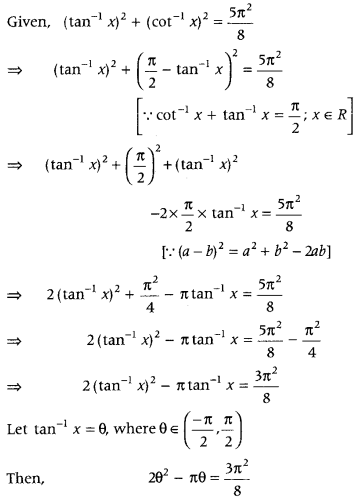
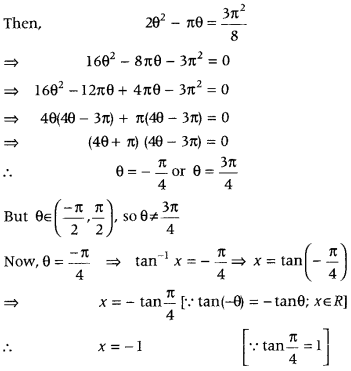
Question 43.
Prove the following.
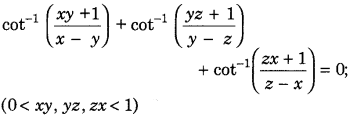
(All India 2015)
Answer:
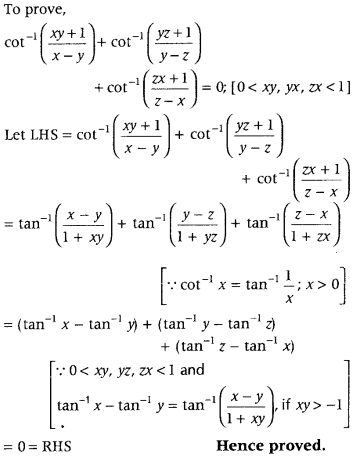
Question 44.
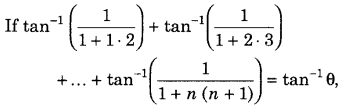
then find the value of θ. (Foregin 2015)
Answer:
First, convert each inverse trigonometric function in the form, of tan-1(x−y1+xy)1 and then use the formula tan-1 (x−y1+xy) = tan-1x – tan-1 y; xy > – 1 Further, simplify it and again use the above formula.
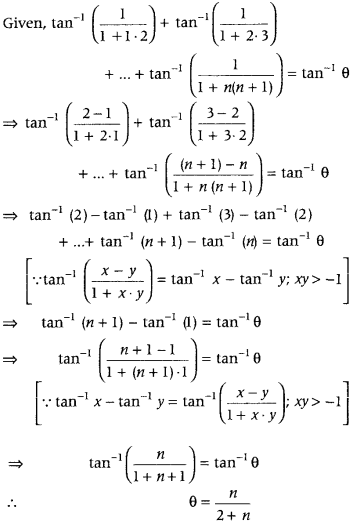
Question 45.
Prove that
2 tan-1(12) + tan-1(17) = sin-1(31252√) (All India 2015C)
Answer:
First, use the relation,
2 tan-1 x = tan-1(2x1−x2); – 1 < x < 1 and then use tan-1 x + tan-1y = tan-1(x+y1−xy); xy < 1
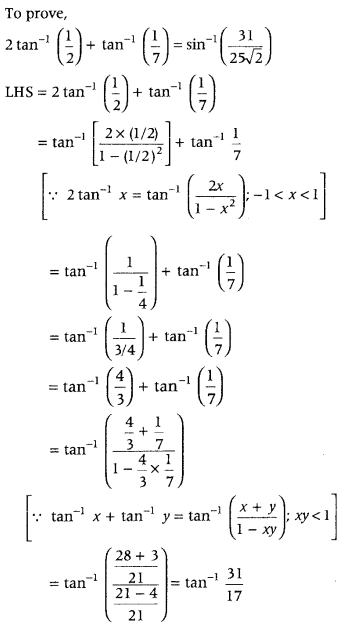

Question 46.
Solve the following equation for x.
tan-1(1−x1+x) = 12tan-1x, x > 0
(All India 2015C, 2O14C, 2010, 2009C; Foreign 2011C, 2008C)
Answer:

⇒ 3x2 = 1 ⇒ x2 = 13
⇒ x = ± 13√
[∵ x > 0 given, so we do not take x = – 13√]
[∴ x = 13√ is the only solution of the given equation.]
Question 47.
Solve for x, tan-1x + 2 cot-1 x = 2π3. (All India 2014C; Delhi 2009C)
Answer:
Given equation is tan-1 x + 2 cot-1 x = 2π3
Then, the given equation can be written as
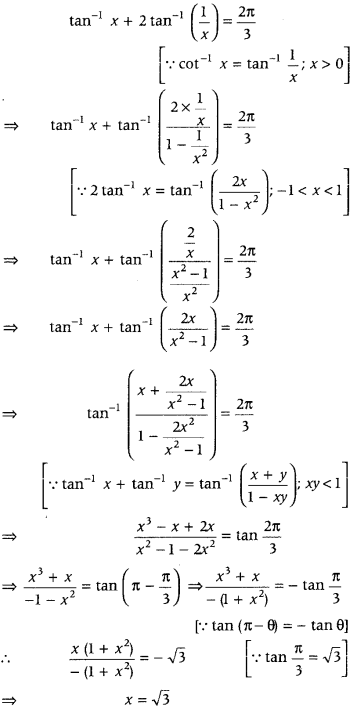
Question 48.
Prove that
2 tan-1(15) + sec-1(52√7) + 2 tan-1(18)=π4. (Delhi 2014)
Answer:
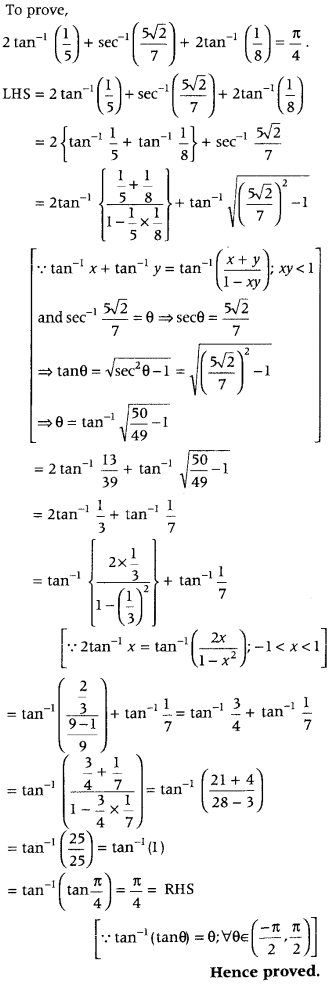
Question 49.
Prove that tan-1[1+x√−1−x√1+x√+1−x√] = π4−12 cos-1x, – 12√ ≤ x ≤ 1. (All India 2014, 2014C, 2011)
Answer:
To prove,
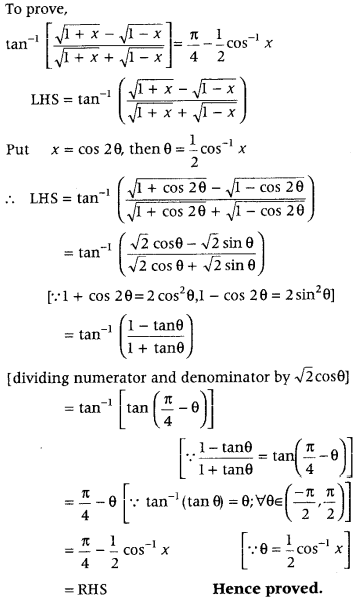
Question 50.
If tan-1 (x−2x−4) + tan-1 (x+2x+4) then find the value of x. (All India 2014)
Answer:
x = ± √2
Question 51.
Prove that
cos-1 (x) + cos-1{x2+3−3x2√2} = π3. (All India 2014C)
Answer:
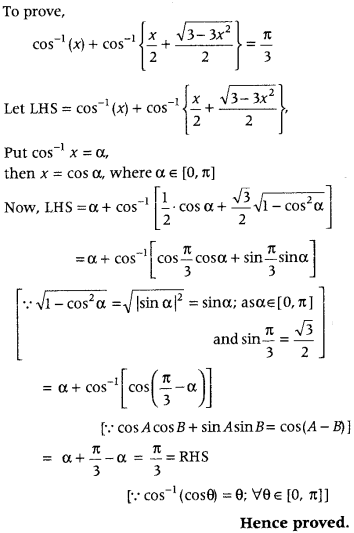
Question 52.
Prove that
cot-1 7 + cot-1 8 + cot-1 18 = cot-1 3. (Forei9n 2014)
Answer:
To prove. cot-1 7 + cot-1 8 + cot-1 18 = cot-1 3
LHS = cot-1 7 + cot-1 8 + cot-1 18
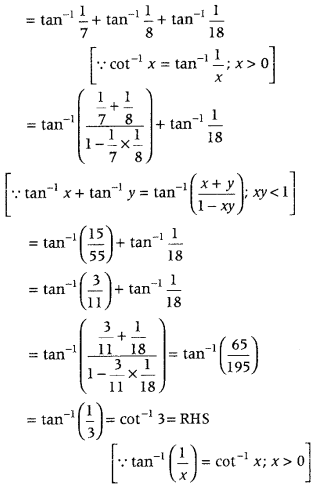
Hence proved.
Question 53.
Prove that
sin-1(817) + sin-1(35) = cos-1(3685). (All India 2014C; Delhi 2012, 2010C)
Answer:

Question 54.
Show that tan(12sin−134)=4−7√3. (All India 2013).
Answer:


Question 55.
Solve for x, sin-1 (1 – x) – 2 sin-1 x = π2. (All India 2013C)
Answer:
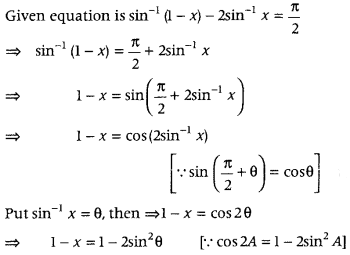
⇒ 1 – x = 1 – 2x2 [∵ sin-1 x = θ ⇒ x = sin θ]
⇒ 2x2 – x = 0
⇒ x(2x – 1) = 0
∴ x = 0 or x = 12
For x = 12 , LHS = sin-1(12) – 2 sin-1(12)
= π6−2π6=−π6≠π2
∴ x = 12 is not a solution of given equation.
Hence, x = 0 is the only solution. (1)
Question 56.
Prove that sin-1817 + sin-135 = tan-17736. (Delhi 2013C)
Answer:

Question 57.
Find the value of the following. (Delhi 2013)
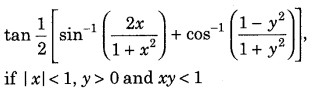
Answer:
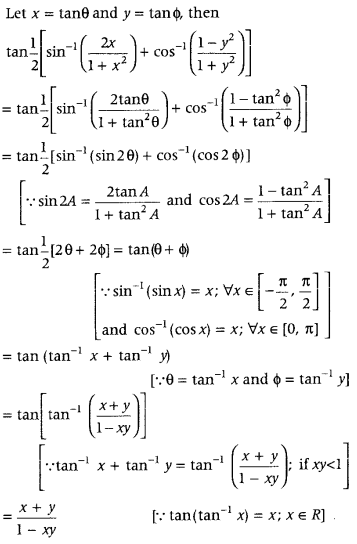
Question 58.
Prove that (Delhi 2013; All India 2011, 2008C)
![]()
Answer:

Question 59.
Prove that (Delhi 2012)
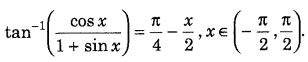
Answer:
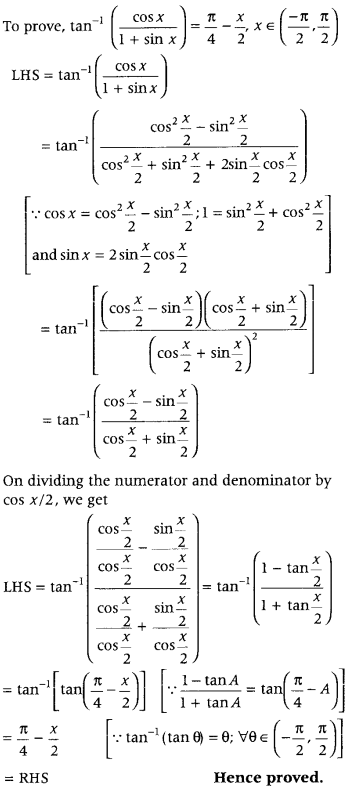
Question 60.
Prove that (All India 2012; Delhi 2010C, 2009)
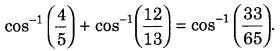
Answer:
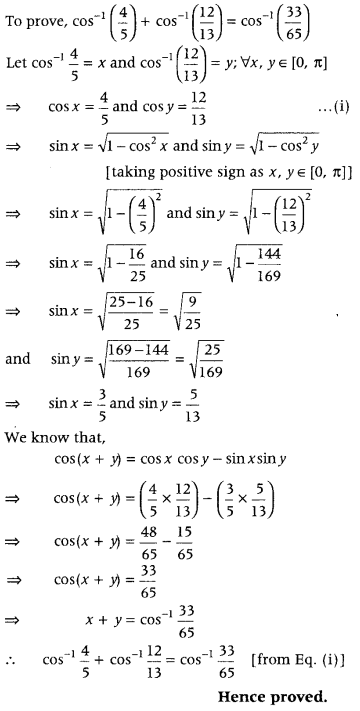
Question 61.
Prove the following. (All India 2012)
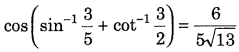
Answer:

Question 62.
Prove that
sin-1(6365) = sin-1(513) + cos-1(35). (Foregin 2012).
Answer:
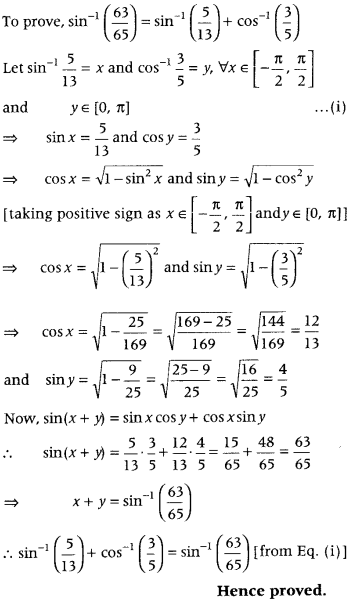
Question 63.
Solve for x ,
2 tan-1(sin x) = tan-1(2 sec x), x ≠ π2. (Foregin 2012)
Answer:
π4
Question 64.
Find the value of
tan-1(xy) – tan-1(x−yx+y) (Delhi 2011)
Answer:
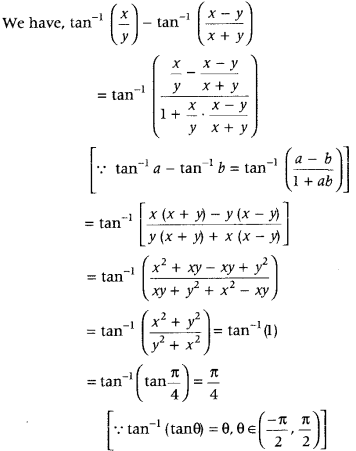
Question 65.
Prove that (All India 2011; Delhi 2009C, 2008C)
2 tan-1(12) + tan-1(17) = tan-1(3117).
Answer:
First, use the relation,
2 tan-1 x = tan-1(2x1−x2); – 1 < x < 1 and then use tan-1 x + tan-1y = tan-1(x+y1−xy); xy < 1
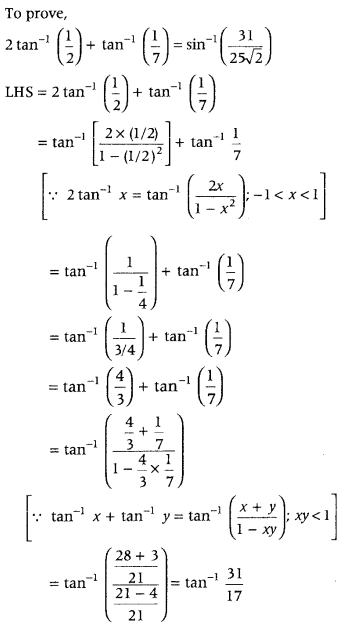

Question 66.
Prove that (Foregin 2011)
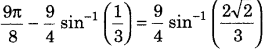
Answer:
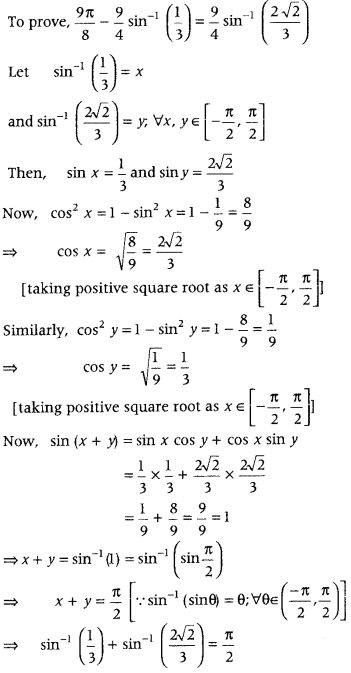
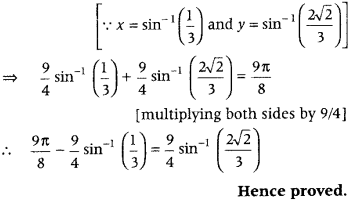
Alternate Method:
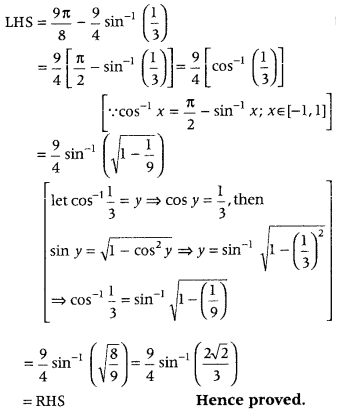
Question 67.
Prove that tan-1 14 + tan-1 29 = 12 tan-1 43. (All India 2011C)
Answer:
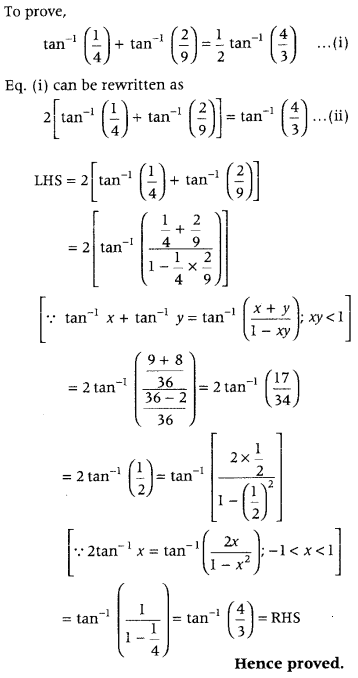
Question 68.
Solve for x, cos (2 sin-1 x) = 19; x > 0. (All India 2011C)
Answer:
Given equation is
cos (2 sin-1 x) = 19 , x > 0 ……. (i)
Put sin-1x = y
⇒ x = sin y
Then, Eq. (1) becomes, cos 2y = 19
⇒ 1 – 2 sin2 y = 19 [∵ cos 2θ = 1 — 2s1n2 01(1)
⇒ 2 sin2 y = 1 – 19 = 89
⇒ sin2 y = 49
⇒ x2 = 49 [∵ sin y = x]
∴ x = ± 23 [taking square root]
But it is given that, x > 0.
∴ x = 23
Question 69.
Prove that 2 tan-1 34 – tan-1 1731=π4. (Delhi 2011C)
Answer:
First, use the relation
2 tan-1 x = tan-1(2x1−x2) – 1 < x < 1 and then use the relation tan-1 x – tan-1 y = tan-1 (x−y1+xy), xy > – 1 and get the required result.
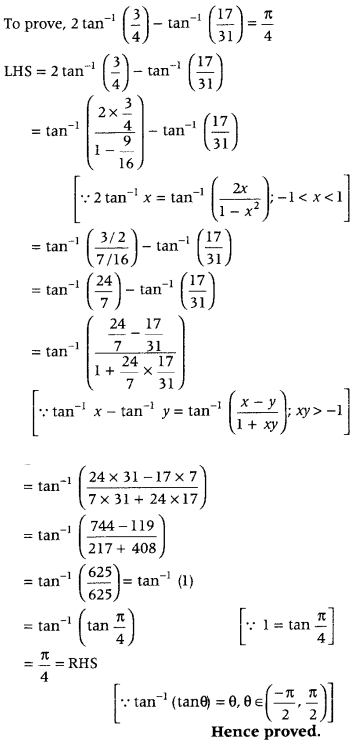
Question 70.
Solve for x,
tan-1(2x1−x2) + cot-1(1−x22x) = π3, – 1 < x < 1. (Delhi 2011C)
Answer:
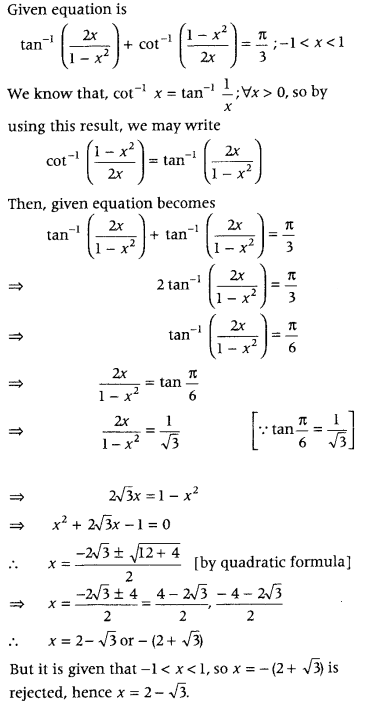
Question 71.
Prove that
tan-1 √x = 12 cos-1(1−x1+x) , x ∈ (0, 1). (Delhi 2010)
Answer:
First, put √x = tan θ ⇒ θ = tan-1 √x and then use cos 2θ = 1−tan2θ1+tan2θ

Question 72.
Prove that (Delhi 2010)
cos-1(1213) + sin-1(35) = sin-1(5665)
Answer:
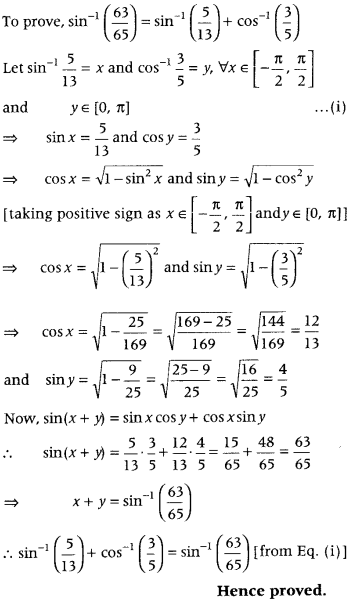
Question 73.
Prove that
tan-1(1) + tan-1(2) + tan-1(3) = π. (Delhi 2010)
Answer:
To prove,
tan-1(1) + tan-1(2) + tan-1(3) = π
LHS = tan-1(1) + tan-1(2) + tan-1(3)
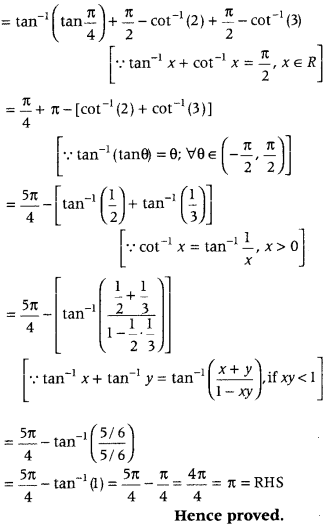
Question 74.
Prove that
tan-1x + tan-1(2x1−x2) = tan-1(3x−x31−3x2). (All India 2010).
Answer:

Question 75.
Prove that
cos [tan-1{sin(cot-1 x)}] = 1+x22+x2−−−−√. (All India 2010).
Answer:
To prove, cos [tan-1 {sin (cot-1x}] = 1+x22+x2−−−−√
LHS = cos (tan-1 {sin(cot-1 x)}]
Put cot-1 x = θ ⇒ x = cot θ
Then, LHS = cos (tan-1 (sin θ)]
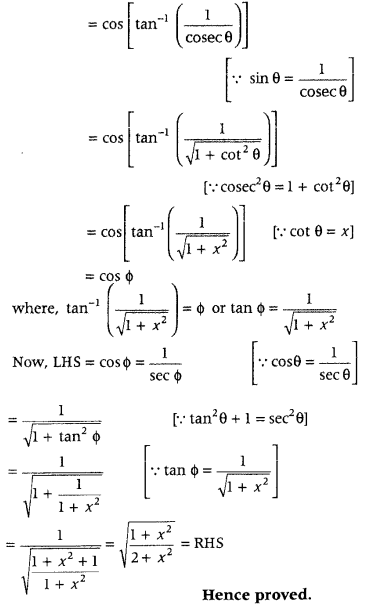
Question 76.
Solve for x, cos-1x + sin-1(x2) = π6. (All India 2010C)
Answer:
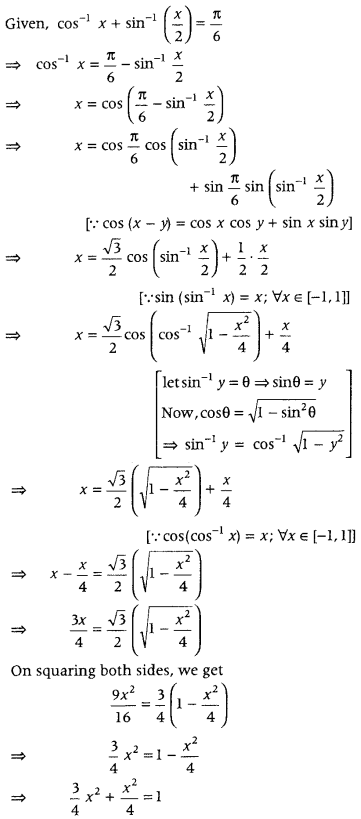
⇒ 4x24 = 1
∴ x2 = 1 ⇒ x = ± 1
But x = -1, does not satisfy the given equation.
Hence, x = 1 satisfy the given equation.
Question 77.
Prove that
2 tan-1 13 + tan-1 17=π4. (All India 2010C)
Answer:
First, use the relation
2 tan-1 x = tan-1(2x1−x2) – 1 < x < 1 and then use the relation tan-1 x – tan-1 y = tan-1 (x−y1+xy), xy > – 1 and get the required result.
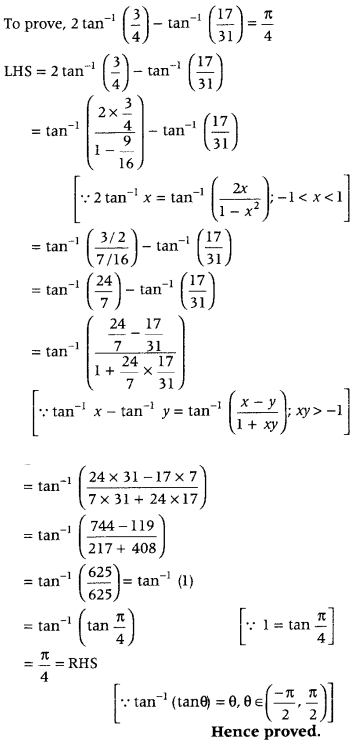
Question 78.
Solve for x, tan-1x2 + tan-1x3=π4, (√6 > x > 0. (Delhi 210C)
Answer:
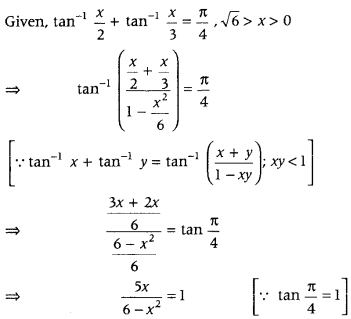
⇒ 5x = 6 – x2
⇒ x2 + 5x – 6 = 0
⇒ x2 + 6x – x – 6 = 0
⇒ x(x + 6) – 1(x + 6) = 0
⇒ (x – 1) (x + 6) = 0
∴ x = 1 or – 6
But it is given that. √6 > x > 0 ⇒ x > 0
∴ x = – 6 is rejected.
Hence. x =1 is the only solution of the given equation.
Question 79.
Solve for x, tan-1(x + 2) + tan-1(x – 2) = tan-1(879), x > 0 (Delhi 2010C)
Answer:
First, use the formula tan-1 x + tan-1 y = tan-1(x+y1−xy); xy < 1, then simplify it and get the values of x. Further, verify the given equation by obtained values of x.
Given, tan-1(x + 1) + tan-1(x – 1) = tan-1 831 …… (i)
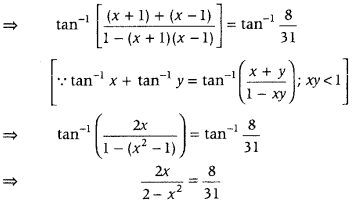
⇒ 62x = 16 – 8x2
⇒ 8x2 + 62x – 16 = 0
⇒ 4x2 + 31x – 8 = 0
⇒ 4x2 + 32x – x – 8 = 0
⇒ 4x(x + 8) – 1 (x + 8) = 0
⇒ (x + 8) (4x – 1) = 0
∴ x = -8 or x = 14
But x = – 8 gives LHS = tan-1 (- 7) + tan-1 (- 9)
= – tan-1 (7) – tan-1 (9),
which is negative, while RHS is positive.
So, x = – 8 is not possible.
Hence, x = 14 is the only solution of the given equation.


Recent Comments