Matrices Class 12 Important Questions with Solutions Previous Year Questions
Matrix and Operations on Matrices
Question 1.
If 3A – B = [5101] and B = [4235] then find the value of matrix A. (Delhi 2019)
Answer:
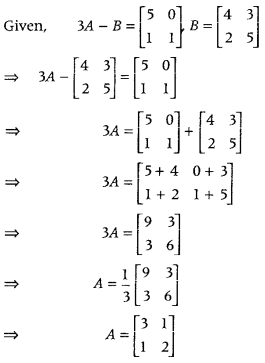
Question 2.
Find the value of x – y, if (Delhi 2019)
2[103x]+[y102]=[5168]
Answer:
Given that,
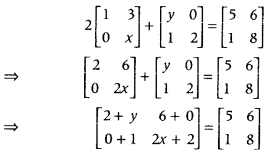
Here, both matrices are equal, so we equate the corresponding elements,
2 + y = 5 and 2x + 2 = 8
⇒ y = 3 and 2x = 6 ⇒ x = 3
Therefore, x – y = 3 – 3 = 0
Question 3.
If A is a square matrix such that A2 = I, then find the simplified value of (A – I)3 + (A + I)3 – 7A. (Delhi 2016)
Answer:
Given, A2 = 7 ……. (i)
Now, (A – I)3 + (A + I)3 – 7A
= (A3 – 3A2I + 3AI2 – I) + (A3 + 3A2I + 3AI2 + I3) – 7A
= A3 – 3A2 + 3AI – I + A3 + 3A2 + 3AI + I – 7A
[∵ A2I = A2 and I3 = I3 = I]
= 2A3 + 6AI – 7A = 2A2 A + 6A – 7A [∵ AI = A]
= 2IA – A [from Eq. (1)]
= 2A – A = A [∵ IA = A]
Question 4.
Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3. (All India 2016)
Answer:
We know that, a matrix of order 2 × 2 has 4 entries. Since, each entry has 3 choices, namely 1, 2 or 3, therefore number of required matrices
34 = 3 × 3 × 3 × 3 = 81.
Question 5.
If [2 1 3] ⎡⎣⎢−1−10011−101⎤⎦⎥⎡⎣⎢10−1⎤⎦⎥ = A, then write the order of matrix A. (Foregin 2016)
Answer:
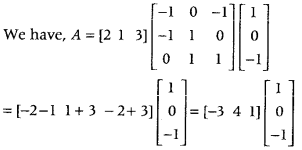
= [- 3 – I] = [- 4]1 × 1
∴ Order of matrix A is 1 × 1.
Question 6.
Write the element a of a 3 × 3 matrix A = [aij], whose elements are given by aij = |i−j|2 (Delhi 2015)
Answer:
Given, A = [aij]3 × 3
where, aij = |i−j|2
Now, a23 = |2−3|2=|−1|2=12
[put i = 2 and j = 3]
Question 7.
If [2x 3] [1−320] [x3] = 0, find x. (Delhi 2015C)
Answer:
Given, matrix equation is
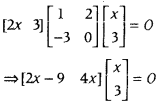
⇒ [2x2 – 9x + 12x] = [0]
⇒ 2x2 + 3x = 0
⇒ x(2x + 3) = 0
∴ x = 0 or x = – 3/2
Question 8.
If 2[354x]+[10y1]=[71005], then find (x – y). (Delhi 2014)
Answer:
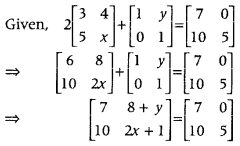
On equating the corresponding elements, we get
8 + y = 0 and 2x + 1 = 5
⇒ y = – 8 and x = 5−12 = 2
∴ x – y = 2 – (-8) = 10
Question 9.
Solve the following matrix equation for x.
[x 1] [1−200] = 0 (Delhi 2014)
Answer:
Given, [x1][1−200] = 0
By using matrix multiplication, we get
[x – 2 0] = [0 0]
On equating the corresponding elements, we get
x – 2 = 0
⇒ x = 2
Question 10.
If A is a square matrix such that A2 = A, then write the value of 7A — (I + A)3, where I is an identity matrix. (All India 2014)
Answer:
Given, A2 = A
Now, 7A – (I + A)3 = 7A – [I3 + A3 + 3I4(I + A)]
[∵ (x + y)3 = x3 + y3 + 3xy (x + y)]
= 7A – [I + A2.A + 3A(I + A)]
[∵ I3 = I and IA = A]
= 7A – (I + A . A + 3AI + 3A2)
[∵ A2 = A]
= 7A – (I + A + 3A + 3A)
[∵AI = A and A2 = AI]
= 7A – (I + 7A) = – 1
Question 11.
If [x−y2x−yzw]=[−1045], then find the value of x + y. (All India 2014)
Answer:
Given
[x−y2x−yzw]=[−1045]
On equating the corresponding elements, we get
x – y = – 1 …… (i)
and 2x – y = 0 …… (ii)
On solving the Eqs.(i) and (ii), we get
x = 1 and y = 2
∴ x + y = 1 + 2 = 3
Question 12.
If [a+483b−6]=[2a+28b+2a−8b], then write the value of a – 2b. (Foreign 2014)
Answer:
Given,
[a+483b−6]=[2a+28b+2a−8b]
On equating the corresponding elements, we get
∴ a + 4 = 2a+ 2 ……… (i)
3b = b + 2 ……. (ii)
and – 6 = a – 8b ……… (iii)
On solving the Eqs. (i), (ii) and (iii), we get
a = 2 and b = 1
Now, a – 2b= 2 – 2(1) = 2 – 2 = 0
Question 13.
If [x⋅yz+64x+y]=[80w6], then write the value of (x + y + z). (Delhi 2014C)
Answer:
Given,
[x⋅yz+64x+y]=[80w6]
On equating the corresponding elements, we get
∴ x – y = 8 ……. (i)
Z + 6 = 0
⇒ z = – 6 ……… (ii)
and x + y = 6 ……… (iii)
Now, on adding Eqs. (ii) and (iii), we get
x + y + z = 6 + (- 6) = 0
Question 14.
The elements a of a 3 × 3 matrix are given by aij = 12|- 3i + j|. Write the value of element a32. (All India 2014C)
Answer:
72
Question 15.
If [2x 4][x−8] = 0, then find the positive value of x. (All India 2014C)
Answer:
Given,
[2x 4][x−8] = 0
On equating the corresponding elements, we get
⇒ 2x2 – 32 = 0
⇒ 2x2 = 32
⇒ x2 =16
⇒ x = ±4
∴ Positive value of x is 4.
Question 16.
If 2[103x]+[y102]=[5168] then find the value of(x + y). (Delhi 2013C; All India 2012)
Answer:
8
Question 17.
Find the value of a, if (Delhi 2013)
[a−b2a−b2a+c3c+d]=[−10513]
Answer:
1
Question 18.
If [9−2−1143] = A + [1024−19], then find the matrix A. (Delhi 2013)
Answer:
Given, matrix equation can be rewritten as
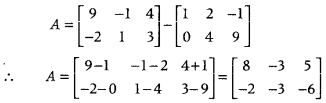
NOTE: Two matrices can be subtracted only when their orders are same.
Question 19.
If matrix A = [1−1−11] and A2 = kA. then write the value of k. (All India 2013)
Answer:

Question 20.
If matrix A = [2−2−22] and A2 = pA. then write the value of p. (All India 2013)
Answer:
19
Question 21.
If matrix A = [3−3−33] and A2 = λA, then write the value of λ. (All India 2013)
Answer:
19
Question 22.
Simplify
cos θ [cosθ−sinθsinθcosθ] + sin θ [sinθcosθ−cosθsinθ] (Delhi 2012)
Answer:
First, multiply each element of the first matrix by cos θ and second matrix by sin θ and then use the matrix addition.
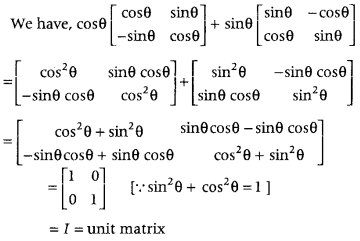
Question 23.
If [2537][1−2−34]=[−4−96x], write the value of x. (Delhi 2012)
Answer:
Given matrix equation is
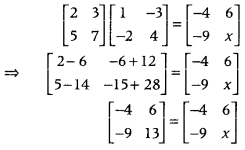
On equating the corresponding elements, we get
x = 13
Question 24.
Find the value of y – x from following equation.
2[x75y−3]+[31−42]=[715614] (All India 2012)
Answer:
7
Question 25.
If x[23]+y[−11]=[105], then write the value of x. (Foreign 2012)
Answer:
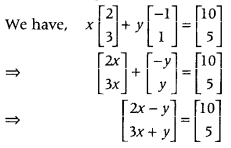
On equating the corresponding elements, we get
2x – y = 10 …… (i)
and 3x + y = 5 …… (ii)
On adding Eqs. (i) and (ii), we get
5x = 15
∴ x = 3
Question 26.
If 3A – B = [5101] and B = [4235], then find the matrix A. (Delhi 2012C)
Answer:
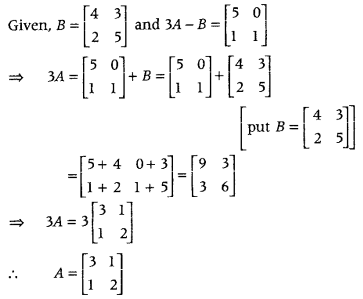
Question 27.
Write the value of x – y + z from following equation. (Foregin 2011)
⎡⎣⎢x+y+zx+zy+z⎤⎦⎥=⎡⎣⎢957⎤⎦⎥
Answer:
Given matrix equation is
⎡⎣⎢x+y+zx+zy+z⎤⎦⎥=⎡⎣⎢957⎤⎦⎥
On equating the corresponding elements, we get
x + y+ z = 9 …… (i)
x + z = 5 …….. (ii)
and y + z = 7 ……. (iii)
On putting the value of x + z from Eq. (ii) in Eq. (i), we get
y + 5 = 9 ⇒ y = 4
On putting y = 4 in Eq. (iii), we get z = 3
Again, putting z = 3 in Eq. (ii), we get x = 2
∴ x – y + z = 2 – 4 + 3 = 1
Question 28.
Write the order of product matrix (Foreign 2011)
⎡⎣⎢123⎤⎦⎥[234]
Answer:
Use the fact that if a matrix A has order m × n and other matrix B has order n × z, then the matrix AB has order m × z.
Let A = ⎡⎣⎢123⎤⎦⎥ and B = [2, 3, 4]
Here, order of matrix A = 3 × 1
and order of matrix B = 1 × 3
∴ Order of product matrix AB = 3 × 3
Question 29.
If a matrix has 5 elements, then write all possible orders it can have. (All India 2011)
Answer:
Use the result that if a matrix has order m × n, then total number of elements in that matrix is mn.
Given, a matrix has 5 elements. So, possible order of this matrix are 5 × 1 and 1 × 5.
Question 30.
For a 2 × 2 matrix, A = [aij] whose elements are given by aij = i/j, write the value of a12. (Delhi 2011)
Answer:
12
Question 31.
If [x2x+yx−y7] = [3817], then find the value of y. (Delhi 2011C)
Answer:
Given,
[x2x+yx−y7] = [3817]
On equating the corresponding elements, we get
x = 3 and x – y = 1
⇒ y = x – 1 = 3 – 1 = 2
Question 32.
From the following matrix equation, find the value of x. (Foreign 2010)
[x+y−543y]=[3−546]
Answer:
Given
[x+y−543y]=[3−546]
On equating the corresponding elements, we get
x + y = 3 … (i)
and 3y = 6 …. (ii)
From Eq. (ii), we get
y = 2
On substituting y = 2 in Eq. (i), we get
x + 2 = 3
⇒ x = 1
Question 33.
Find x from the matrix equation (Foreign 2010)
[1435][x2]=[56]
Answer:
First, determine the multiplication of matrices in . LHS and then equate the corresponding elements of both sides.
Given matrix equation is
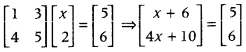
On equating the corresponding elements, we get
x + 6 ⇒ 5 x = – 1
Question 34
If [324x][x1]=[1915], then find the value of x. (Foreign 2010)
Answer:
5
Question 35.
If A = [cosαsinα−sinαcosα] then for what value of α, A is an identity matrix? (Delhi 2010)
Answer:
First, put the given matrix A equal to an identity matrix and then equate the corresponding elements to get the value of α.
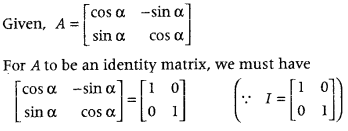
On equating the element a11 of both matrices, we get
cos α = 1
⇒ cos α = cos 0° [∵ cos 0° = 1]
∴ α = 0
Hence, for α = 0, A is an identity matrix.
[∵ sin 0 = 0]
Question 36.
If [1324][3215]=[7k1123], then write the value of k, (Delhi 2010)
Answer:
17
Question 37.
If A is a matrix of order 3 × 4 and B is a matrix of order 4 × 3, then find order of matrix (AB). (DelhI 2010C)
Answer:
3 × 3
Question 38.
If [x+y2y15]=[7415],then find the value of x. (Delhi 2010C)
Answer:
x = 5
Question 39.
If [2x+y03y4]=[6004], then find the value of x. (All India 2010C)
Answer:
x = 3
Question 40.
If [3y−x3−2x7]=[53−27], then find the value of y. (All India 2010C)
Answer:
y = 2
Question 41.
If A = [4−121], show that (A – 2I) (A – 3I) = 0. (All IndIa 2019C)
Answer:
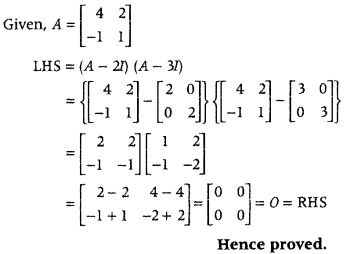
Question 42.
Find a matrix A such that 2A – 3B + 5C = 0, where B = [−232104] and C = [2701−26]. (Delhi 2019)
Answer:
Given, 2A – 3B + 5C = 0 ⇒ 2A = 3B – 5C
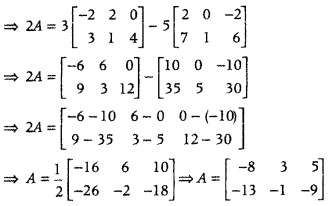
Question 43.
If A = ⎡⎣⎢22101−1130⎤⎦⎥ then find the values of (A2 – 5A). (Delhi 2019)
Answer:
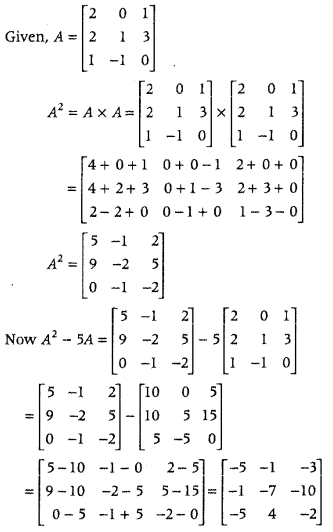
Question 44.
Find matrix A such that (All India 2017)
⎡⎣⎢21−3−104⎤⎦⎥A=⎡⎣⎢−119−8−222⎤⎦⎥
Answer:
Let the order of A is m × n ∴ m = 2, n = 2
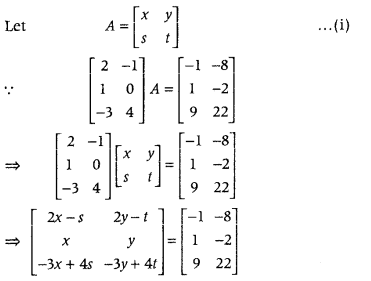
On equating corresponding elements both sides, we get
2x – s = – 1, x = 1, y = – 2 and 2y – t = – 8
At x = 1, 2x – s = – 1 ⇒ 2 × 1 – s = – 1
⇒ – s = – 1 – 2 = s = 3 and at y = – 2, 2y – t = – 8,
⇒ 2 × (- 2) – t = – 8
⇒ – 4 – t = – 8
⇒ t = 4
On putting x = 1, y = – 2, s = 3 and t = 4 in Eq. (i),
we get A = [13−24]
Question 45.
Let A = [23−14], B = [5724], C = [2358], find a matrix D such that CD – AB = 0. (Delhi 2017)
Answer:

Question 46.
If A = ⎡⎣⎢22101−1130⎤⎦⎥, then find A2 – 5A + 4I and hence find a matrix X such that A2 – 5A + 4I + X = 0. (Delhi 2015)
Answer:
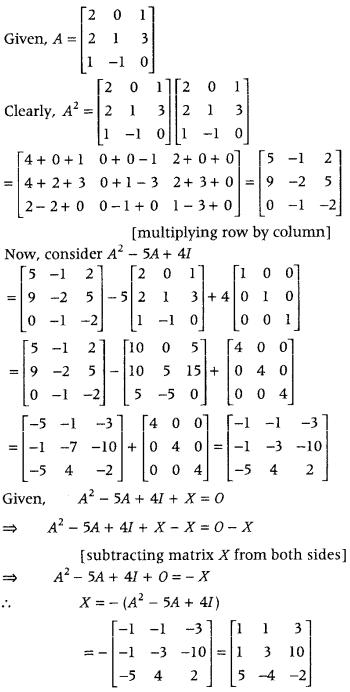
Question 47.
If A = [12−1−1], B = [ab1−1] and (A + B)2 = A2 + B2, then find the values of a and b. (Foreign 2015)
Answer:
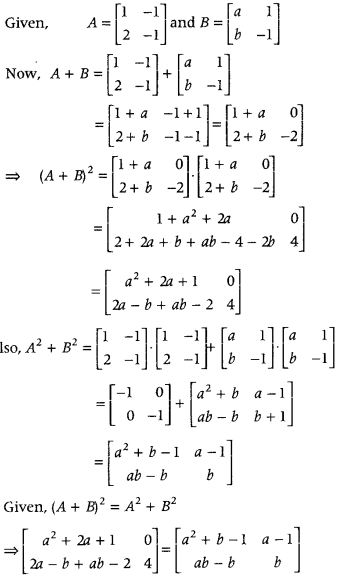
On equating the corresponding elements, we get
a2 + 2a + I = a2 + b – 1 ⇒ 2a – b = – 2
a – 1 = 0 ⇒ a = 1 ….. (ii)
2a – b + ab – 2 = ab – b
⇒ 2a – 2 = 0 ⇒ a = 1 ….. (iii)
and b = 4 …….(iv)
Since, a = 1 and b = 4 also satisfy Eq. (1). therefore
a = 1 and b = 4
Question 48.
If A = ⎡⎣⎢22101−1130⎤⎦⎥, then find value of A2 – 3A + 2I. (All India 2010)
Answer:
⎡⎣⎢13−3−1−32−1−40⎤⎦⎥
Question 49.
If A = ⎡⎣⎢102020213⎤⎦⎥ and A3 – 6A2 + 7A + kI3 = 0, find the value of k. (All India 2016)
Answer:
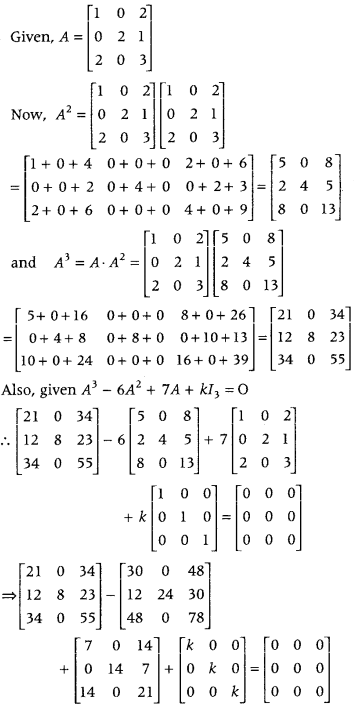
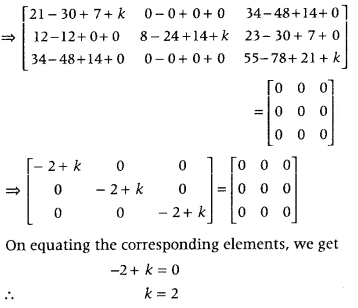
Transpose of a Matrix, Symmetric and Skew-Symmetric Matrices
Question 1.
If A = ⎡⎣⎢12−22122x−1⎤⎦⎥ is a matric satisfying AA’ = 9I, find x. (CBSE 2018C)
Answer:
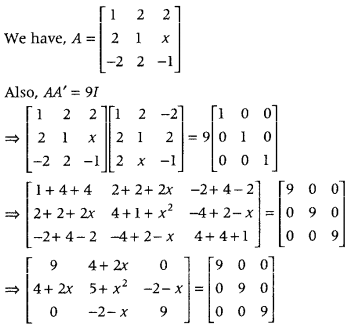
On equating the corresponding elements, we get
4 + 2x = 0 and 5 + x2 = 9
⇒ x = – 2 and x2 = 4
⇒ x = – 2 and x = ±2
∴ The value of x is -2
Question 2.
If the matrix A = ⎡⎣⎢02ba01−3−10⎤⎦⎥ is skew-symmetric, find the values of ‘a’ and ‘b’. (CBSE 2018)
Answer:

Question 3.
Matrix A = ⎡⎣⎢033a2b13−23−1⎤⎦⎥ is given to be symmetric, find the values of a and b.
Answer:

Question 4.
If A = [cosα−sinαsinαcosα], then find a satisfying 0 < α < π2 when A + AT = √2 I2;
where AT is transpose of A. (All India 2016)
Answer:
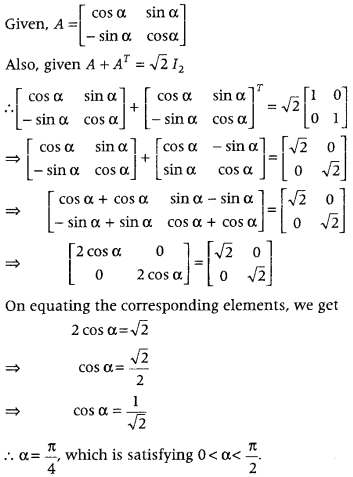
Question 5.
If A = (3759) is written as A = P + Q, where P is a symmetric matrix and Q is skew-symmetric matrix, then write the matrix P. (Foreign 2016)
Answer:
We have A = (3759) and A = P + Q. where P is symmetric matrix and Q is skew-symmetric matrix.
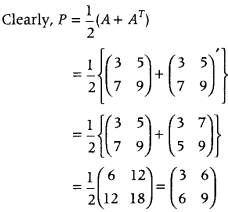
Question 6.
Write 2 × 2 matrix which is both symmetric and skew-symmetric. (Delhi 2014C)
Answer:
A null matrix of order 2 × 2, i.e. [0000] is both symmetric and skew-symmetric.
Question 7.
For what value of x, is the matrix A = ⎡⎣⎢0−1x10−3−230⎤⎦⎥ a skew-symmetric matrix? (All India 2013)
Answer:
If A is a skew-symmetric matrix, then A = – AT, where AT is transpose of matrix A.

Question 8.
If AT = ⎡⎣⎢3−10421⎤⎦⎥ and B = [−112213], then find AT – BT (All India 2012)
Answer:
First, find the transpose of matrix 6 and then subtract the corresponding elements of both matrices AT and BT.
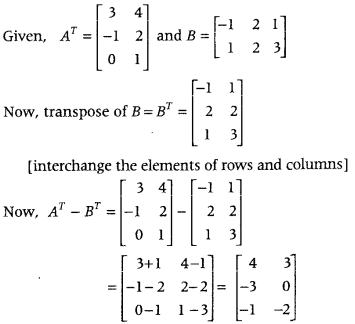
Question 9
If A = [1324], then find A + A’. (All India 2010C)
Answer:
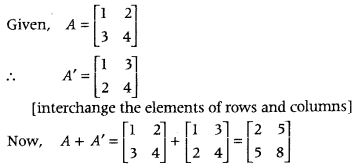
Question 10.
If (2x+y03y4)=(6604), then find the value of x. (All India 2010)
Answer:
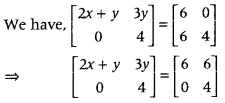
We know that, if two matrices are equal, then their corresponding elements are equal.
∴ 2x + y = 6 ….. (i)
and 3y = 6 ….. (ii)
From Eq. (ii), we get
y = 2
On substituting y = 2 in Eq. (i), we get
2x+ 2 = 6
⇒ x +1 = 3
∴ x = 2
Question 11.
Show that all the diagonal elements of a skew-symmetric matrix are zero. (Delhi 2017)
Answer:
Let A = [aij] be a skew-symmetric matrix.
Then, aij = – aij for all i, j
Now, put i = j, we get
⇒ aii = – aii for all values of i
⇒ 2 aii = 0
⇒ aii = 0 for all values of i
∴ a11 = a22 = a33 = ….. = ann = 0
Hence, all the diagonal elements of a skew symmetric matrix are zero.
Hence proved.
Question 12.
Express the matrix A = ⎡⎣⎢27143−2−654⎤⎦⎥ as the sum of a symmetric and skew-symmetric matrix. (All India 2015C)
Answer:
Any square matrix A can be expressed as the sum of a symmetric matrix and skew-symmetric matrix, i.e.
A = A+A′2+A−A′2, where A+A′2 and A−A′2
are symmetric and skew-symmetric matrices, respectively.

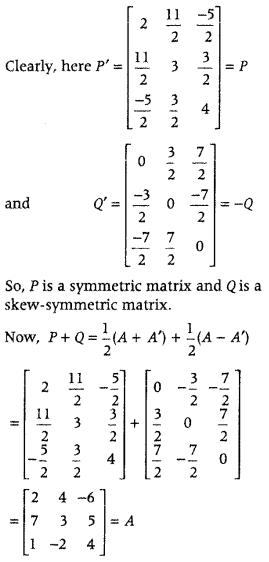
Thus, matrix A is expressed as the sum of symmetric matrix and skew-symmetric matrix.
Question 13.
For the following matrices A and B, verify that [AB]’ = B’A’;
A = ⎡⎣⎢1−43⎤⎦⎥, B = [-1 2 1]. (All India 2010).
Answer:

Question 14
Express the following matrix as a sum of a symmetric and a skew-symmetric matrices and verify your result: (All India 2010)
⎡⎣⎢33−1−2−21−4−52⎤⎦⎥
Answer:
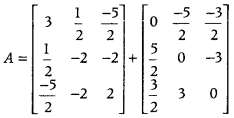
Inverse of a Matrix by Elementary Operations
Question 1.
Use elementary column operation C2 → C2 – 2C1 in the matrix equation. (Foreign 2014)
[4323]=[1023][2101]
Answer:
Apply the given operation on the matrix of LHS and the second matrix of RHS,
Given matrix equation is
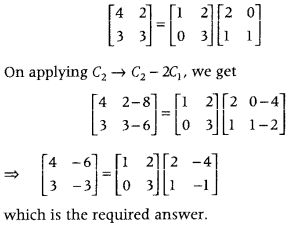
Question 2.
Using elementary row transformations (ERT), find inverse of matrix (Foreign 2010)
A = [6554].
Answer:
First, write the matrix A as A = IA. Then, by applying elementary row transformations on A of LHS and same on I of RHS. convert the given matrix equation in the form of I = BA, where B gives the inverse of A.
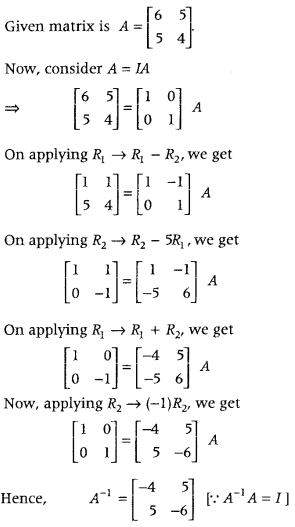
Question 3.
Find A-1, by using elementary row transformations for matrix A = [3725] (Foreign 2010)
Answer:
A-1 = [5−7−23]
Question 4.
Using elementary row transformations, find inverse of matrix A = [2153] (Delhi 2010)
Answer:
A-1 = [3−1−52]
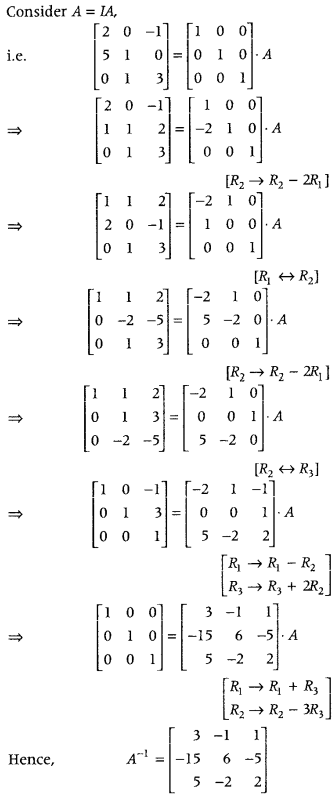
Question 5.
A = ⎡⎣⎢250011−103⎤⎦⎥ (All India 2019; Foregin 2011)
Answer:
Question 6.
A = ⎡⎣⎢−113121231⎤⎦⎥ (Delhi 2019; 2012)
Answer:
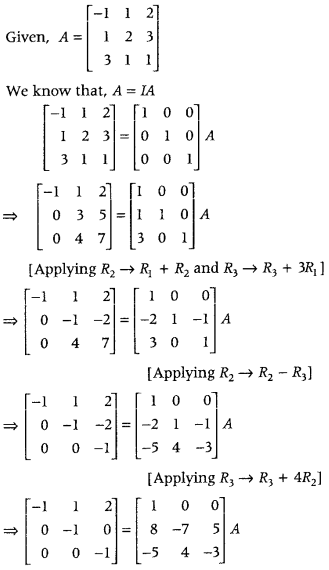
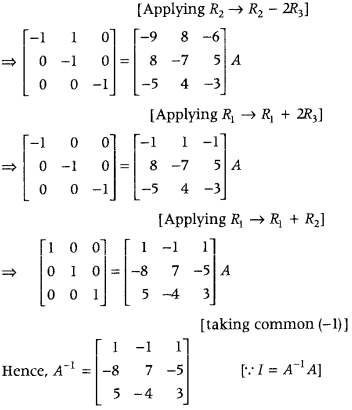
Question 7.
A = ⎡⎣⎢1−1023−2−201⎤⎦⎥ (Delhi 2019; 2018C; 2010)
Answer:
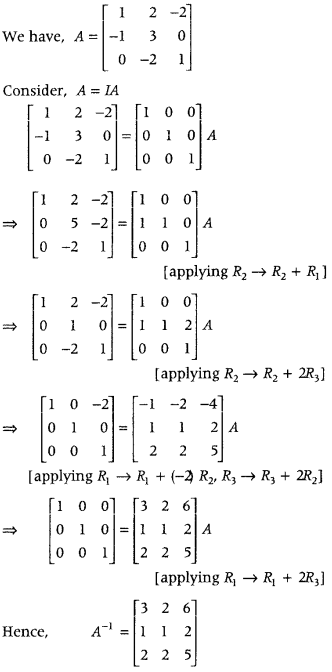
Question 8.
A = ⎡⎣⎢12−225−437−5⎤⎦⎥ (CBSE 2018)
Answer:
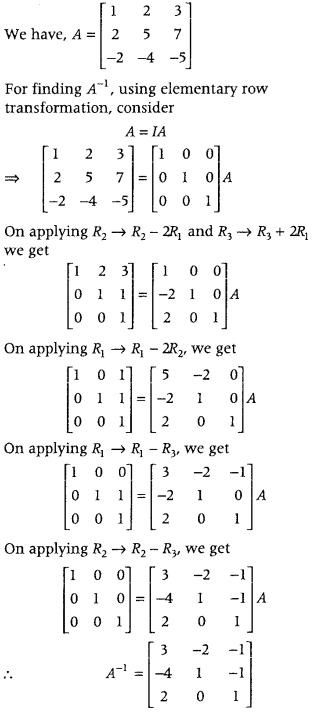
Question 9.
A = ⎡⎣⎢1−32301−2−10⎤⎦⎥ (Delhi 2011)
Answer:
A-1 = ⎡⎣⎢1−2−3−245−379⎤⎦⎥

Recent Comments